Hi,
There was a time when I believed in Saint Nicholas, the Dutch equivalent of Santa Claus.
One day, long after December, I walked into my father’s office. And there I saw them hanging: the drawings I had made for the saint and put in my shoe – as is tradition – a few months before.
"How did they get there?" I asked my dad, pointing at my drawings.
"Oh yes," answered my father with a nonchalance that still impresses me to this day, "St Nicholas lost them when he walked through the house."
I was reassured.
But then a St Nicholas came to visit us who looked suspiciously like our neighbour Jaap. And when I went looking, I found wrapped gifts hidden in my brother’s room.
The evidence was too overwhelming: I no longer believed in St Nicholas.
Update your beliefs
We all have beliefs. Ideally, we adapt them when new relevant information becomes available. As economist John Maynard Keynes is supposed to have said: "When the facts change, I change my mind. What do you do, sir?"
(The quote is often attributed to Keynes, but the words cannot be traced back to him.)
Take the facts about coronavirus. Do face masks help? How long are you immune after being infected? Does the virus spread via aerosols? These are all subjects we are gradually learning more about.
Like me and my understanding of St Nicholas, scientists probably have a hypothesis. Yes, no, maybe ... And as more evidence becomes available, they adapt their view. This is also called "belief updating".
But how do you do it? A minister from the 18th century has an answer to that.
What are the chances that St Nicholas exists?
Thomas Bayes was an English minister and mathematician. After his death Richard Price published his notes containing a gem, Bayes theorem.
Here it is:
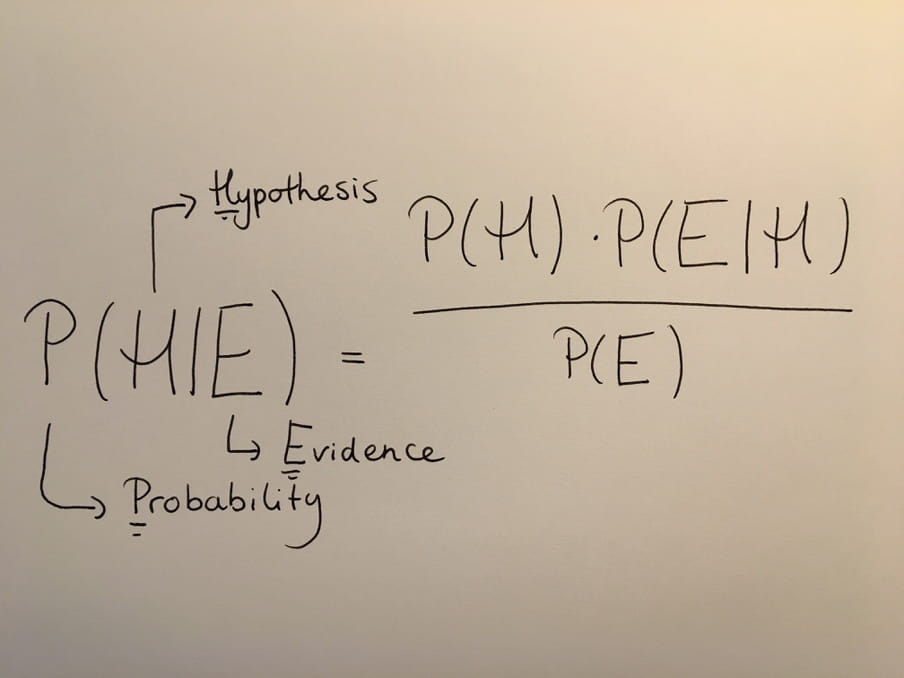
You may not be able to get this right away, but you can probably see how simple the formula is. Just one line. And pretty easy to prove, if you know a thing or two about probability theory.
The H is your hypothesis, in my case that St Nicholas exists. Let’s say that I was pretty sure of my case and that my P(H) – the chance that he is indeed real, that the hypothesis is correct – was equal to 0.9 (90%).
That probability is called the "prior", because it is the probability that you attribute something before new information becomes available.
But then I see the drawings on the wall in my father’s study. Now what is the probability that St Nicholas exists? Bayes theorem helps to calculate that chance. You calculate the P(H|E), the chance that the hypothesis is correct given (that is the vertical dash) that I have seen certain evidence.
This is the "posterior", the probability you give your hypothesis after you have taken more evidence.
To calculate it completely we need some extra ingredients. Namely, the P(E) – the chance that I see those drawings on my father’s wall. For the sake of convenience I assume that my father is such a fan of my work that he hangs all found drawings on the wall. In other words, that probability is 1.
There are now two ways in which I can observe the drawings:
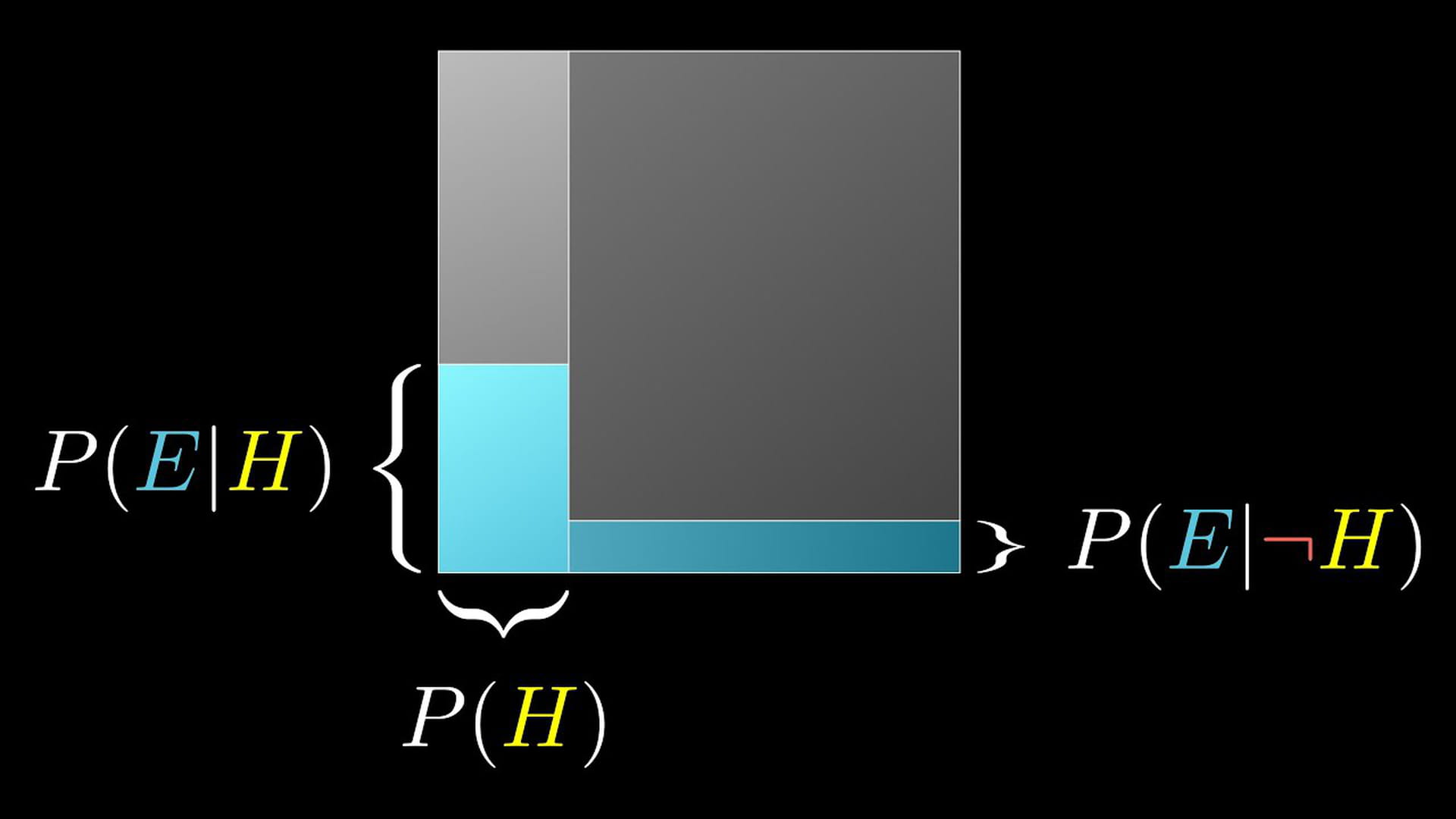
- St Nicholas exists and he loses my drawings (which are guaranteed to end up on my father’s wall). I found it quite astonishing that those drawings were hanging there, so let’s say that, if St Nicholas really existed, I estimated the chance that he would lose my drawings at 0.2. You can write this situation down mathematically as: P(H)*P(E|H)=0.9*0.2=0.18.
- St Nicholas does not exist and I see the drawings hanging on my father’s wall. You can write this down as: P(¬H)*P(E|¬H)=0.1*1=0.1. (That hook means "not", so P(¬H) is the probability that the hypothesis is not correct.)
If we add those two probabilities together, we have the chance that I saw the drawing hanging on the wall: P(E)=0.18+0.1=0.28. Now you can fill in the rest of the formula:
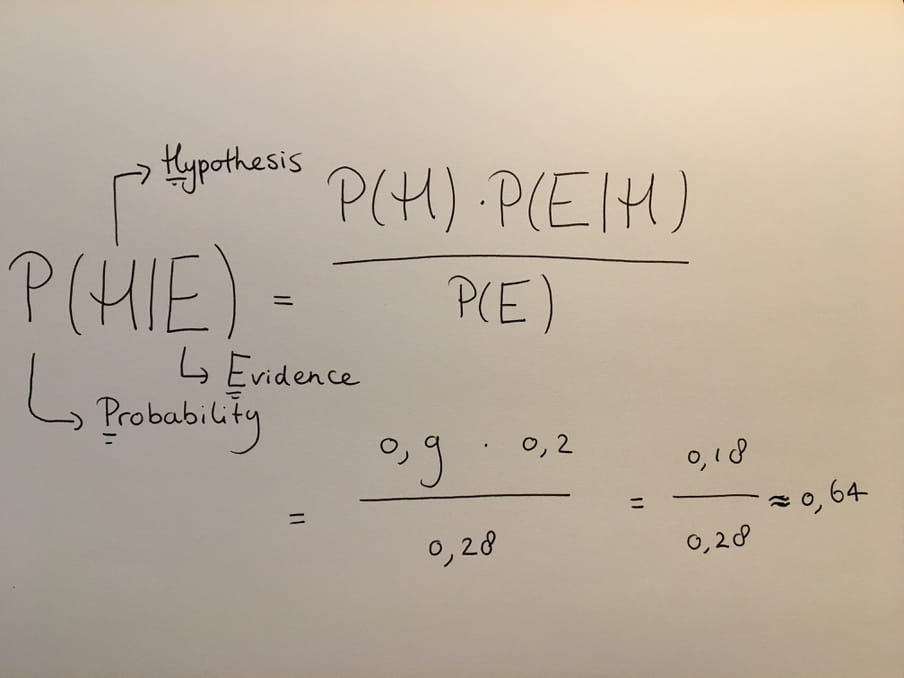
(I used the Dutch notation here, we use commas instead of periods to indicate decimals.)
So my "posterior" is equal to (rounded off) 0.64. At first I had a strong conviction that St Nicholas exists (0.9), now that is less. But still I think there is a greater than 50-50 chance that he does exist. If there were to be another piece of evidence, neighbour Jaap for instance, that could easily flip around.
In this video of 3Blue1Brown you dive further into Bayes theorem:
So what?
It’s not as if I was making those calculations as a child. But the idea behind the process does fit in with how we think. We have prior knowledge, we learn new things, and with that we adapt our image of reality. Whether you use mathematics or not, the lesson is: use new information, but in moderation.
As epidemiologist Marc Lipsitch says: “One extreme is to decide what you think and be impervious to new information. Another extreme is to over-privilege the last thing you learned. In rough terms, Bayesian reasoning is a principled way to integrate what you previously thought with what you have learned and come to a conclusion that incorporates them both, giving them appropriate weights.”
This quote comes from a good article in The New York Times, which explains more about how you can apply Bayesian thinking in the corona crisis.
Pandemics are by no means the only application. The formula is used in lawsuits, in spam filters, in scientific research. Even in treasure hunts the Bayesian approach has proven itself. And do you remember Clippy, the annoying paper clip that bothered you in Windows? It used Bayes too.
Finally, a good tip from statistician David Spiegelhalter. In the same New York Times article he refers to Cromwell’s Law: never assign a 100% or 0% probability to anything. In other words, reserve a little room for doubt.
“Keep a bit back — with a little bit of probability, a little tiny bit — for the fact that you may be wrong,” Spiegelhalter advises. “Then if new evidence comes along that totally contradicts your main prior belief, you can quickly ditch what you thought before and lurch over to that new way of thinking.”’
There is nothing mathematical about that. "... It doesn’t necessarily have to be done technically or formally; it can just be in the back of your mind as an idea. Call it ‘modelling humility.’ You may be wrong.”
So who knows, maybe St Nicholas does exist.
Before you go ...
This month we’re celebrating the very first anniversary of The Correspondent. If you’re a founding member and have yet to renew your membership, you can do so here! Stay tuned for exciting announcements throughout the month, there’s a lot to come.
Not a member yet? You can join now by clicking here and make sure you’re part of all the September fun!
 Prefer to receive this newsletter in your inbox?
Follow my weekly newsletter to receive notes, thoughts, or questions on the topic of numeracy.
Prefer to receive this newsletter in your inbox?
Follow my weekly newsletter to receive notes, thoughts, or questions on the topic of numeracy.
