German chancellor Angela Merkel warned that the health system would be overwhelmed if this number rose above 1.
New Zealand’s prime minister Jacinda Ardern emphasised that by testing, tracing and isolating, the country will keep this number under 1.
And Dutch prime minister Mark Rutte said he wouldn’t hesitate to reintroduce stricter measures if this number becomes higher than 1.
The number they’re talking about? The reproduction number. Governments around the world are basing their policies on this metric.
So it’s time we knew more about it.
What is the reproduction number?
The reproduction number is also called the "transmission rate" or, simply, R. Two terms are often confused: R0 and R.
R0, also called R-nought, is the "basic reproduction number". This is the average number of people that one sick person infects, in a population where the disease first occurs and no measures to prevent the spread of disease have yet been taken. R0 therefore assumes that everyone can still be infected.
The R, on the other hand, is the "effective reproduction number" – the average number of people whom one sick person infects in reality. It is no longer based on the hypothetical starting situation, like R0, but gives an idea of how the disease develops in practice. That’s why it’s the number you want to look at now.
This R is usually smaller than the R0 because, for example, measures have been taken or a vaccine has been found (unfortunately, this is not yet the case for coronavirus). Another difference: R changes over time, R0 is a constant.
How should I interpret the R?
Suppose R is currently equal to 2. This means that one sick person infects two others on average. These in turn each infect two people, making a total of four. So the number of new infections doubles per cycle: 1, 2, 4, 8, 16, 32 ...
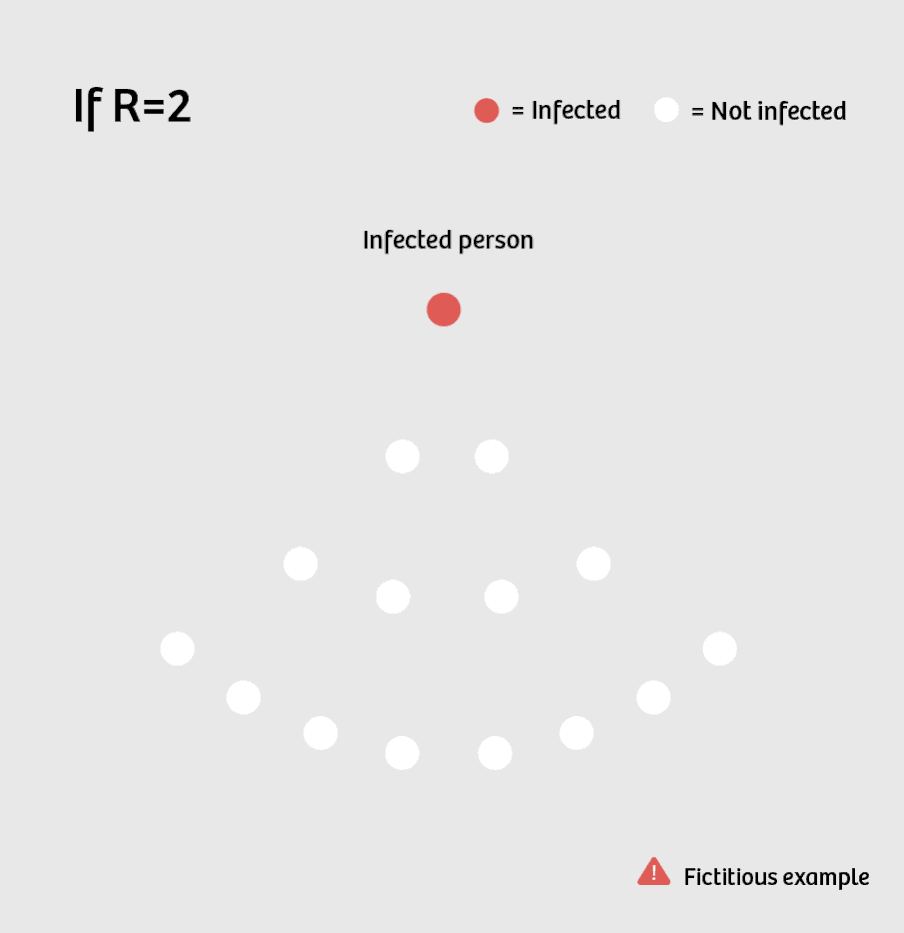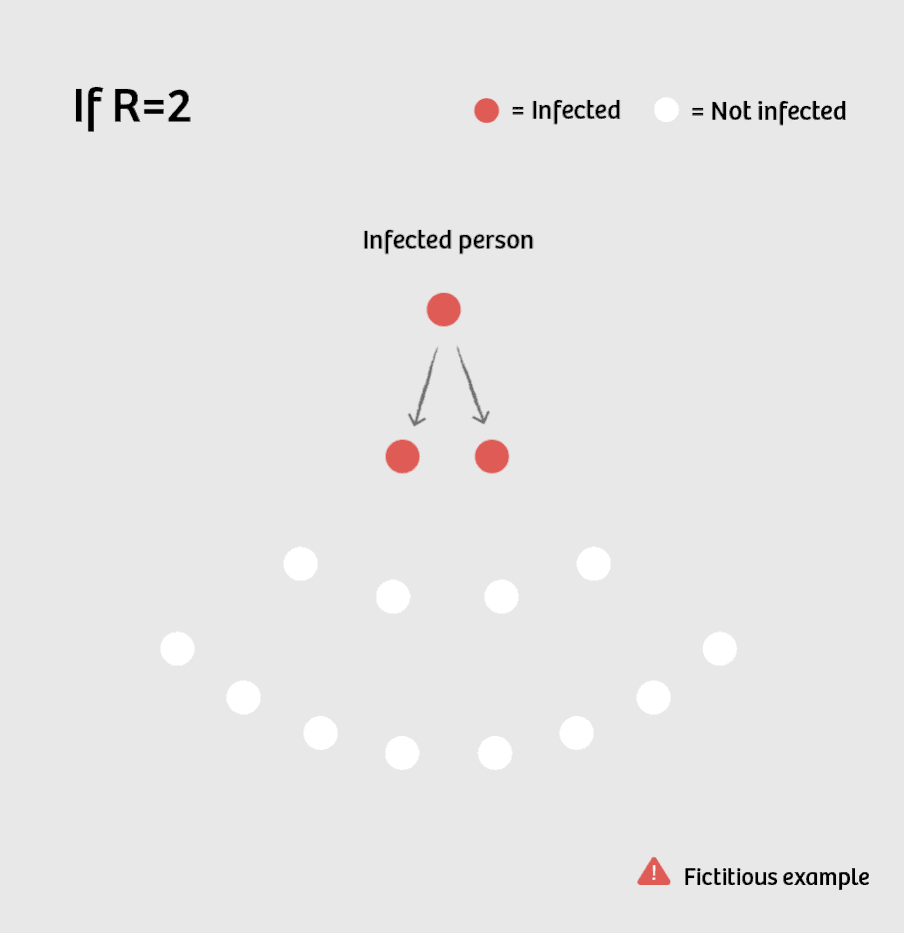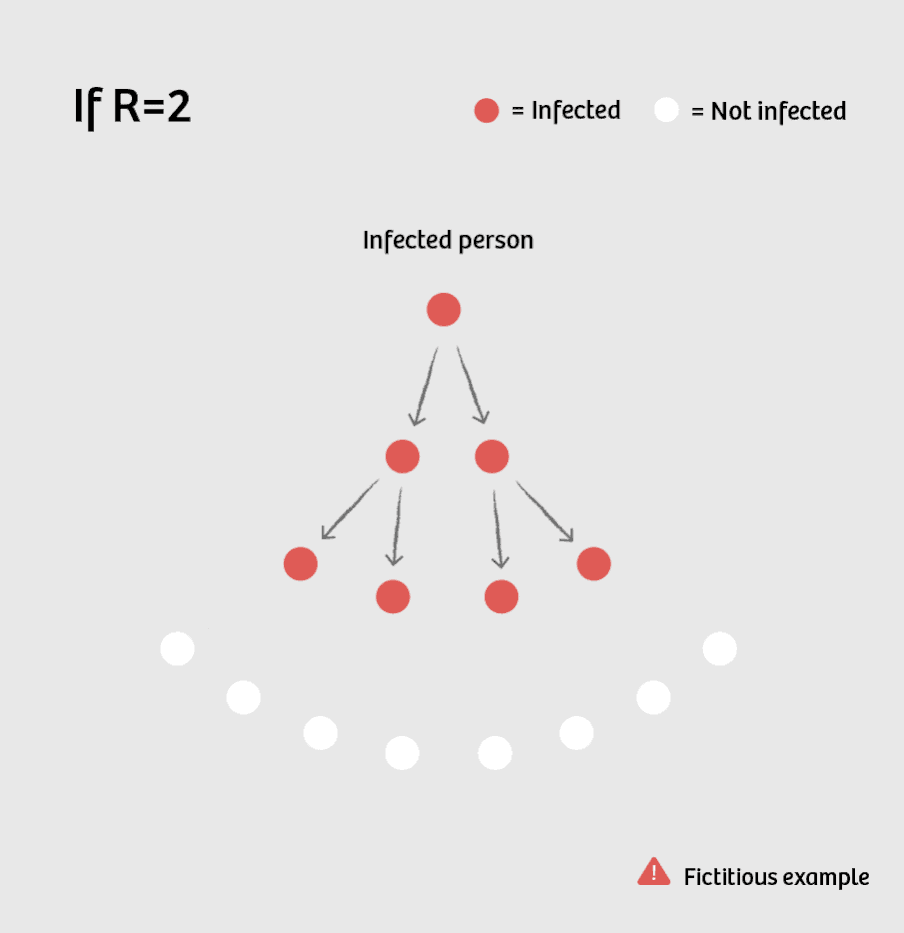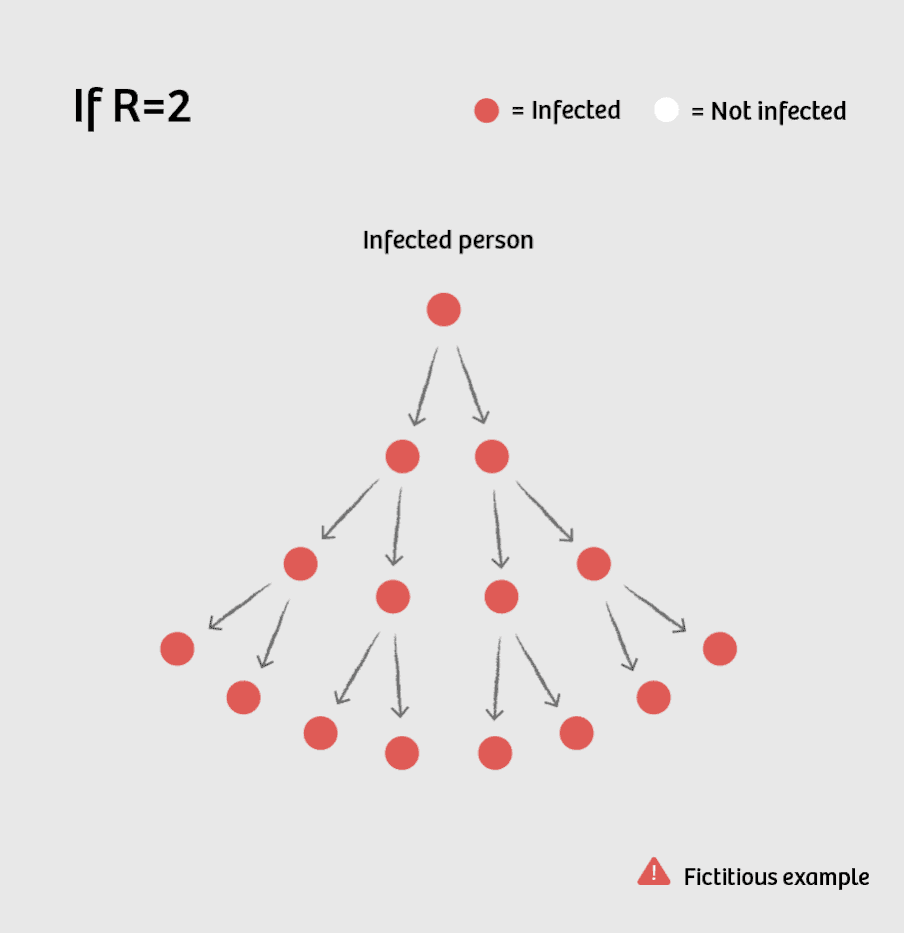
This is what you call exponential growth – a development that doesn’t follow a linear trajectory, but is instead growing faster and faster.
If R equals 1, there is no more increase in new patients, but also no decrease: 1, 1, 1, 1, 1, 1, 1, ... Then the disease is "endemic" – the number of new infections is fairly constant.
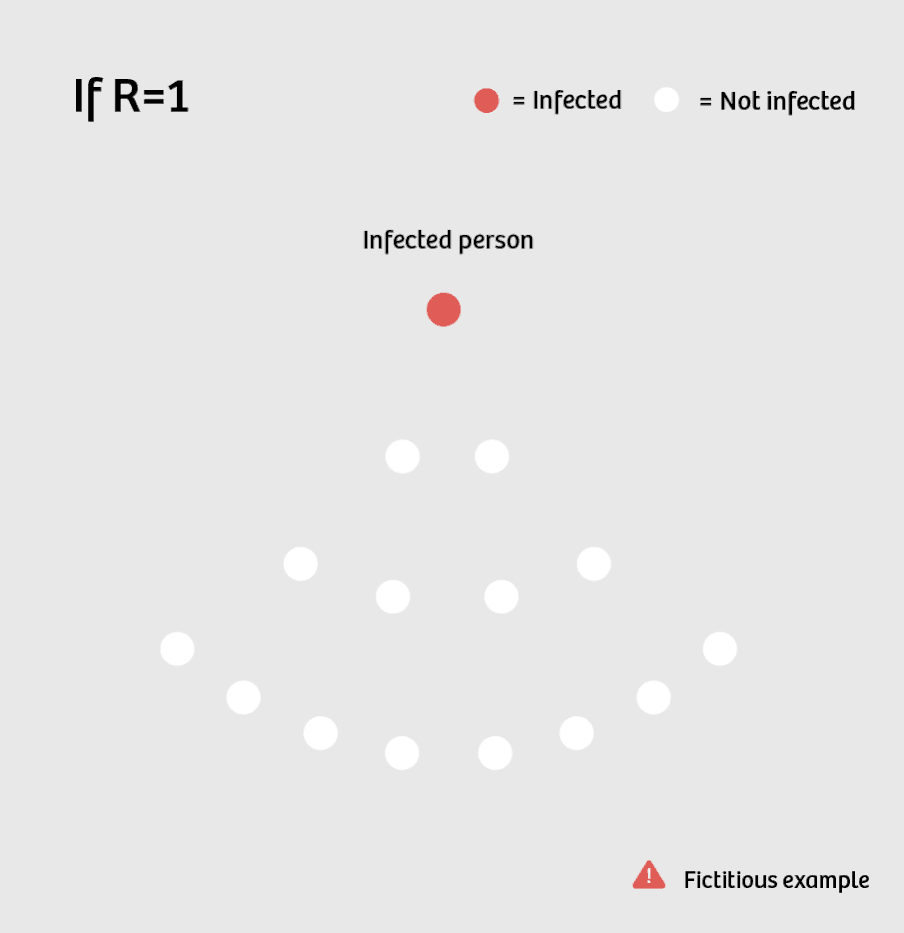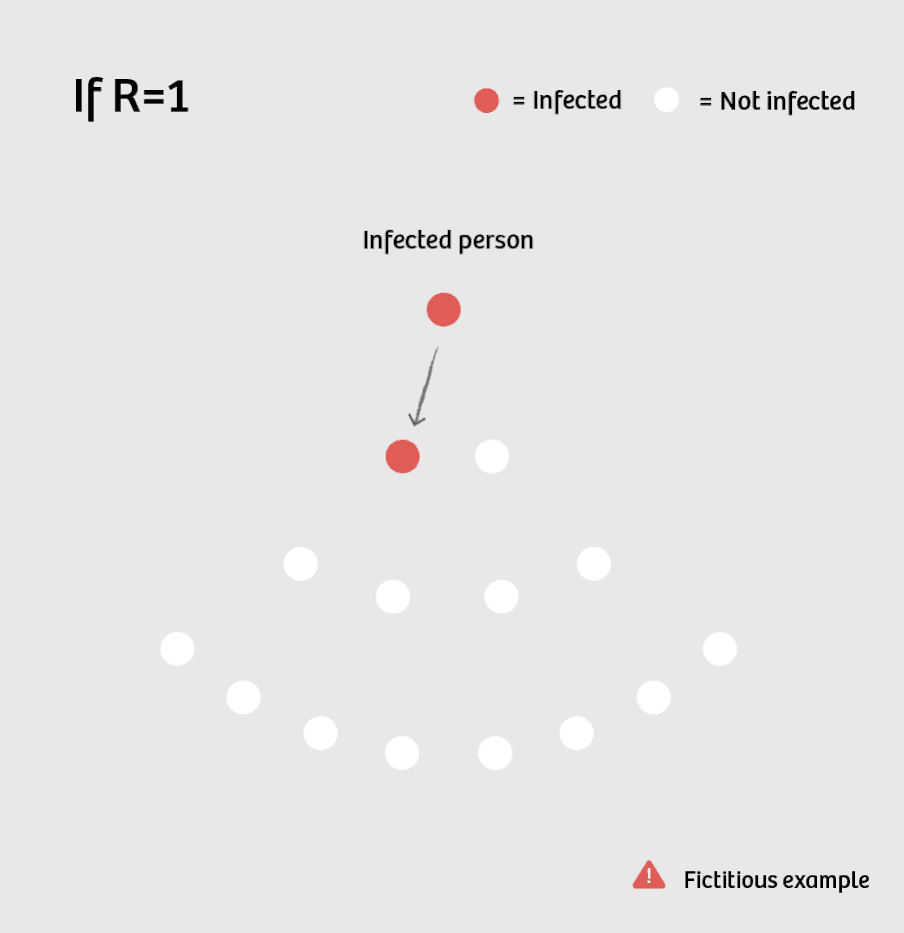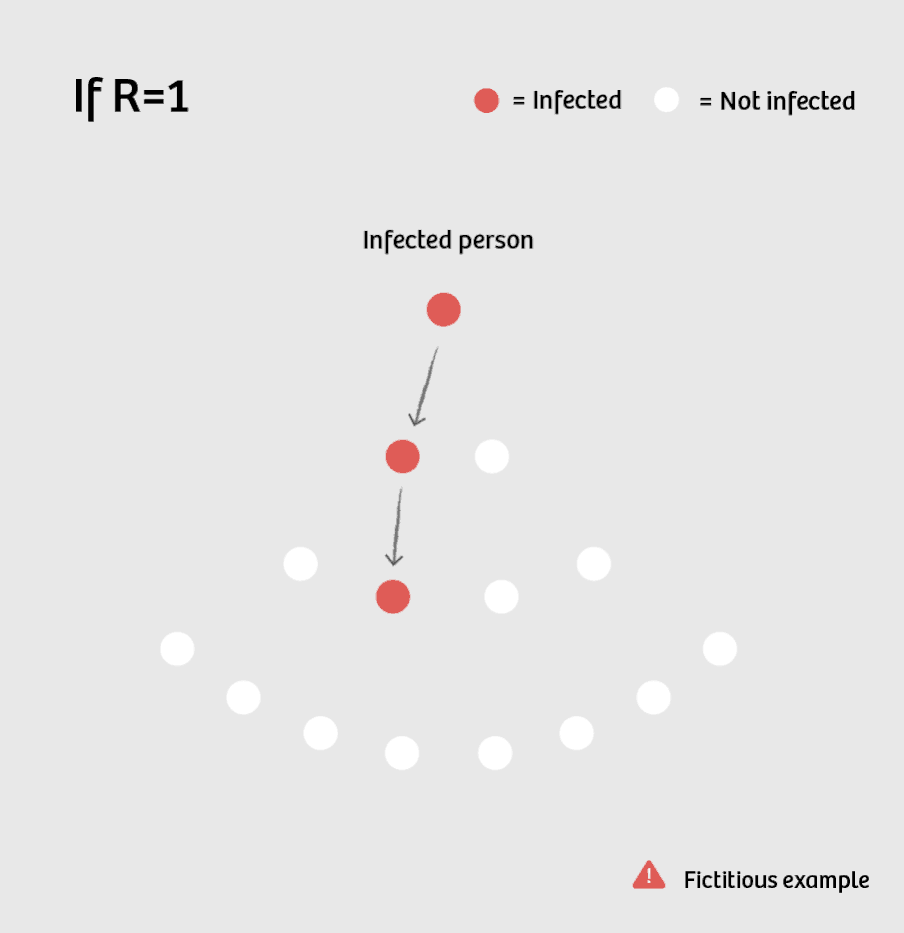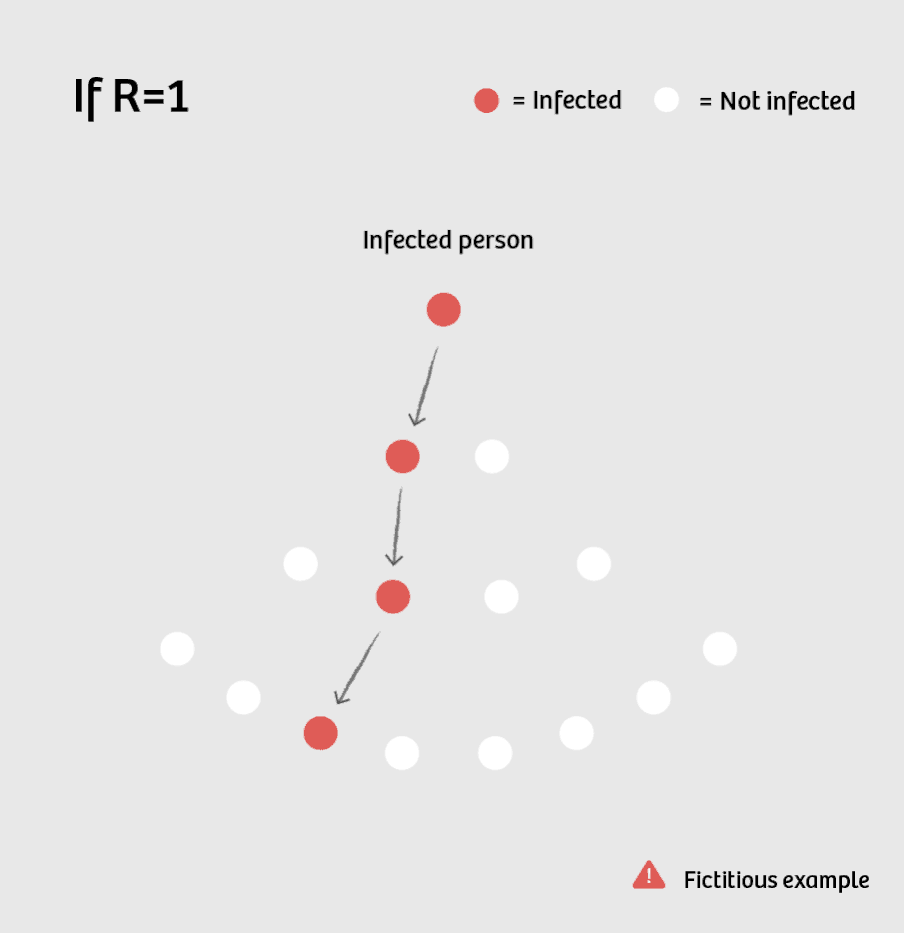
So what governments are aiming for is an R below 1 for their country. On average, each infected person infects fewer than one other person.
Suppose there are 10,000 infectious people in a country and the R is equal to 0.8. Then this is the trajectory of new patients looks like: 10,000, 8,000, 6,400, 5,120, 4,096 ... The disease is petering out.
Preferably, the number goes down to zero, which means that the disease is not detectable any more. But so far, governments are aiming for it to be at least below 1.
If it gets above 1, a small difference like 1.1 and 1.2 can make a huge difference, as Merkel explains in this video.
How do governments’ lockdown measures affect the R?
The R is influenced by three factors:
- The probability that someone infects someone else upon contact (p)
- The number of contacts per unit of time (c)
- The period of time that a person can infect someone (d)
If you multiply those three, you get the R:
The beauty of the formula is that you can see exactly which knobs you can turn if you want to change the R. If you reduce one of the parts, you also reduce the R.
Let’s take the chance of someone infecting someone else (p). You can reduce that probability by washing your hands, keeping your distance, and – hopefully one day – vaccinating people against the disease.
You can reduce the number of contacts per unit of time (c) by working from home, cancelling events, and closing cafes and restaurants.
Finally, the duration of contagiousness (d) can be shortened – for example, by quickly tracing and isolating cases of the disease. That’s why some governments are working on an app, although it’s still unclear how effective such an app would be (leaving aside whether you should want it at all).
How is the R calculated?
The reproduction number is easy to calculate if you know who infected whom. For each patient, you find out how many others that person has infected, you take the average and – voilà – you have your R.
But that method has become unworkable in most countries. There are simply too many cases relative to the number of tests and personnel needed to track all cases. That’s why you need a statistical method that tries to calculate the reproduction number in a different way.
The p*c*d formula is difficult to use because the parts are difficult to estimate. That’s why countries like Germany and the Netherlands draw on the work of Jacco Wallinga, head modeller of the Dutch National Institute for Public Health and the Environment, and Harvard epidemiologist Marc Lipsitch.
An important ingredient for their model is the "generation interval" – the period between the moment someone gets infected and the moment they infect someone else. The general idea: divide the number of people who are sick right now by the number who were sick a generation interval ago – and you have the R.
What data is used?
But then you need to have reliable figures. After all, "garbage in, garbage out". Germany uses the number of new coronavirus cases to calculate the reproduction number.
But that’s a tricky choice because most countries don’t test every suspicious case. That’s why the number of cases and deaths are often an underestimate and – since testing regimes change over time – it’s difficult to know by how much.
That’s why in a country like the Netherlands, where Wallinga is in charge of the model, the method uses records of hospital admissions. Hospitals register the first day of illness, which the modellers use to calculate the reproduction rate.
These hospital data are quite robust because a lot of testing takes place in Dutch hospitals. It’s also important to note that the maximum capacity in hospitals has fortunately never been reached in the Netherlands. So it can be assumed that all serious cases have turned up in these data and that these figures are a good indicator of the proportion of seriously ill patients in the population.
An important point: if certain groups do not come to the hospital – as is sometimes the case for the elderly – then they cannot influence this figure. So this R only says something about the part of the population that can end up in hospital. If there are outbreaks in nursing homes, the actual R will be higher.
How reliable is the R?
The calculation of R is delayed by definition because the first day of illness of new patients is already a few days back from when someone ends up in hospital.
And there is a delay in the registration of cases, especially at weekends. This is why cases only show up a few days later in the data. Also, it’s not always possible to determine with certainty when someone has fallen ill.
All in all, there is certainly some uncertainty in the models, which is why you often see a bandwidth in graphs of R – that’s the margin of uncertainty. So the R could be a bit higher – or a bit lower – than the estimated figure.
And for the most recent period, the uncertainty margin is often so large that you cannot really say anything about the R because of the delays in detection and processing of cases. You’re always looking in the past.
So if the R is below 1, everything is OK?
On 1 March 2003, 23-year-old Esther Sally Mok ended up in Tan Tock Seng Hospital in Singapore. She had returned a few days previous from a trip to Hong Kong and wasn’t feeling well.
Mok would go down in history as the first Sars patient in Singapore. On 25 March, her father died. A day later, her pastor died. Her mother would also die. In total, Mok infected at least 24 people.
The R is only an average. If 35 people do not infect anyone but one person infects 24, as Mok did, then the R is below 1 (24 infections divided by 36 people equals 2/3).
But you see that such outbreaks can occur because a "super spreader" can suddenly infect a lot of people. Another thing: the fact that the R is below 1 does not mean that there are suddenly no new cases. Even with an R of 0.5 (and 10,000 current patients), 5,000 new patients will appear in a few days.
So it’s good to aim for an R below 1, but that that doesn’t mean social distancing will suddenly become a thing of the past.
Want to stay up-to-date?
Follow my weekly newsletter to receive notes, thoughts, or questions on the topic of Numeracy and AI.
Dig deeper
Deciphering the pandemic: a guide to understanding the coronavirus numbers
You’ve already read countless articles on coronavirus infection numbers. But what do those numbers really mean, and how should you read them?